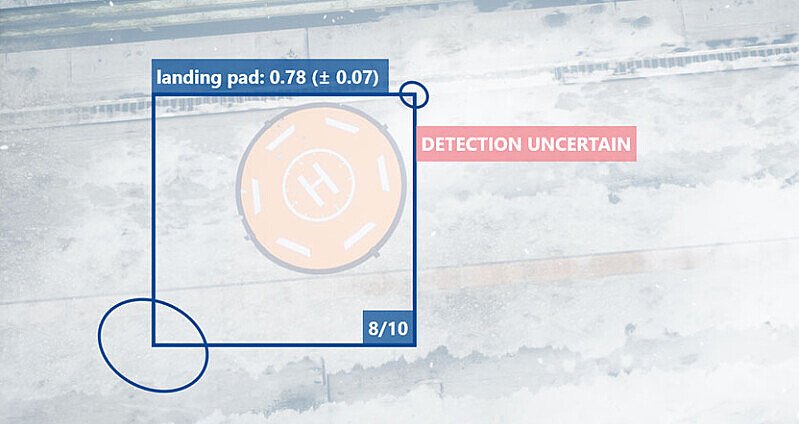
Introduction

In recent years, machine learning (ML) models have become immensely powerful and are used in a wide range of applications and domains. The rise of large language models (LLMs) has led to the popularization of artificial intelligence (AI) in society and boosted the already high interest of the industry. Deep learning models are deployed to estimate depth in 2D images, to predict the number of incidents and needed police deployments, or to convert speech to text, often with impressive results. But regardless of the AI task at hand, the number of parameters, or the used architecture, none of the AI models are perfect. Incorrect predictions and mistakes in outputs generated by the AI are inevitable. The real world is complex, chaotic, dynamically changing, and thus difficult to represent in a training set, from which models gain knowledge. Uncertainty is, therefore, inherent in the model’s operation. For humans it is very natural to express uncertainty when faced with a new situation or a difficult question. We use phrases like “maybe”, “probably” or “I don’t know”. Analogously, the goal of uncertainty quantification (UQ) in ML is to enable the models to signal whether they are confident about the provided output or, on the contrary, that they “don’t know” and are in fact guessing.

In this article, we dive a little bit deeper into the world of UQ in ML and discuss types of uncertainty, methods and approaches that can be used to estimate uncertainties as well as application areas of ML in which uncertainty quantification is helpful. We also describe selected challenges and our latest standardization activities.
 

Types of Uncertainty

Beyond its general, non-technical meaning, uncertainty can be analysed in a more formal way.  A common approach to categorize the uncertainties in ML is to distinguish between epistemic and aleatoric uncertainty. Epistemic uncertainty refers to the lack of knowledge in the model and can stem from insufficient amount of data used in a training or suboptimal architecture choices. Epistemic uncertainty is said to be reducible as it can be explained away by increasing the amount of training data. Aleatoric uncertainty, on the other hand, is related to inherent randomness which can be caused e.g., by measurement noise or stochasticity in the data generation process. Rolling dice is an example of such a process (in fact the word “aleator” means “dice player” in Latin). Aleatoric uncertainty is considered irreducible as gathering and using additional samples is not going to reduce it. While the border between the types and simple distinction between reducible and irreducible is often ambiguous, it is important to be aware of this categorization. Knowing which type of uncertainty should be estimated and which type is quantified by the selected UQ approach can contribute, or even be critical, to the success of the developed system.

Calibration

Uncertainty estimates are only useful if they reflect the empirical level of uncertainty. To illustrate this concept, we can imagine a model that is supposed to recognize car registration plates from camera images automatically without the need to print a ticket, a solution popular in modern parking garages. Let us assume that the used AI model quantifies the uncertainty for each prediction, so that in the uncertain cases (e.g., due to dirty plates, foreign plates, or lack of plates) the driver must take the ticket. Such a system can only function as intended if the model is not assigning high confidences to wrong predictions. If this is not the case, it means that the recognition model is not calibrated or more specifically, overconfident in its predictions. In this scenario, overconfidence can lead to problematic situations during payment but in many other applications it can create serious safety issues. For instance, if an autonomous vehicle is confident but actually wrong about a road sign it has just recognized and acts based on a wrong prediction. ML models can also be underconfident. Severe underconfidence in the parking garage scenario would mean that a lot of drivers are given a ticket, even if their registration plates were recognized correctly. Such behaviour would of course reduce the customer satisfaction and diminish the intended benefits. Ensuring that the uncertainties are calibrated is therefore critical for any decision-making based on the uncertainty measures. But how to check if the model is calibrated? As usual in ML, there are metrics that allow to quantify the level of calibration such as: expected calibration error or quantile calibration error. Furthermore, calibration can also be inspected visually with support of reliability diagrams as the one shown below in Figure 2. By analysing the deviations from the perfect calibration line, reliability diagrams allow to quickly assess whether a model is over- or underconfident.

UQ Approaches and Their Properties

One of the main remaining questions is how to quantify uncertainties in the ML models. The answer is not straightforward as the UQ field is being actively researched and there are no one-size-fits-all solutions. The first possibility is to use probabilistic machine (or deep) learning models i.e., models which inherently provide uncertainties along with the predictions. In other words, they offer built-in uncertainty estimation. Prominent examples are models based on Gaussian processes or Bayesian neural networks. Second alternative is to use approaches that help turn standard models into uncertainty-aware models. An example of an intuitive technique are deep ensembles [1]. The idea behind them is to train a series of models (instead of just one) and for each given input, run inference in all of them. Similarity of the results can be interpreted as a measure of uncertainty. The higher the disagreement between the models, the higher the uncertainty. Many other approaches exist such as Monte Carlo Dropout [2] or methods based on loss function modifications but describing them goes beyond the scope of this introductory blog post. It is important to emphasize that the choice of the UQ approach should be made based on the requirements of the developed model or system.  Different UQ techniques possess different properties such as type of quantified uncertainty or computational complexity (in training or inference). These properties should be considered in the design of the AI system. If the developed model is supposed to run on resource-limited hardware (e.g., on a small drone), running an ensemble of large models may be not feasible.  Lastly, an important aspect is the stage of the AI development process at which UQ can be applied. In practice, we often have access only to an already trained model without possibility to adapt the neural network architecture or to retrain it. Post-hoc UQ approaches such as test-time augmentation or conformal prediction can be of help here.

Applications of UQ

Estimation of uncertainty is useful in various aspects of AI. First, it can be used to improve safety and trustworthiness beyond standard performance evaluation. Checking performance of the model using a test set helps in gaining confidence in model’s generalization capabilities but for obvious reasons performance metrics (such as accuracy or mean squared error) are not available once the model is deployed and operating. Let us consider a drone performing an autonomous landing manoeuvre relying on deep learning-based detection of a landing pad. In a setup without any uncertainty estimation, the detector’s predictions are point estimates (e.g., coordinates of a bounding box). As already mentioned in the calibration chapter (see the parking garage example), if predictions are enriched with uncertainties, these uncertainties can be used to monitor confidence, trigger safety mechanism, request human supervision etc. An AI system, human operator or decision-maker can take the uncertainty of ML prediction into account and adjust actions accordingly. In case of the autonomous drone landing, if the uncertainty is too high, the manoeuvre can be stopped and control can be handed over to a human operator. But applications of UQ go beyond the uncertainty monitoring and are useful in other dimensions of AI such as out-of-distribution detection, reinforcement learning, data fusion (find out more in our AIAA conference paper) or active learning, an approach which we describe in a more detail.

Active learning is a technique that allows to iteratively select samples that should be labelled instead of choosing them randomly or labelling all available samples. It is of high interest especially when the process of obtaining a label is costly. In active learning, a model trained on an initial training set is used to query (request) samples for labelling. Once the new samples are labelled, they are added to the training set. The model is retrained and the procedure is repeated. A core challenge of the whole process is in selecting the query. One approach is to use uncertainty sampling, which loosely speaking means to choose these inputs for which the model is mostly uncertain as they can bring a lot of new information. What is worth mentioning, is the type of uncertainty (see chapter about uncertainty types above)  useful in this scenario. In case of safety monitoring, we might be interested in total uncertainty (it is perhaps not important where the uncertainty is coming from). In active learning, however, epistemic uncertainty is of higher interest as adding samples in regions of high aleatoric uncertainty will not reduce it as described before.

DIN SPEC 92005

Benefits of performing UQ in ML fuel the research and lead to growing awareness of the scientific community. But UQ has also already been investigated in standardization. Initiated by IABG and developed by a consortium of experts, DIN SPEC 92005 “Uncertainty quantification in machine learning” is a standardization document which aims to support stakeholders in adopting UQ in ML. The document defines important terms related to uncertainty and provides an overview of UQ applications, approaches and properties. The core part the DIN SPEC 92005 is a set of recommendations and requirements for incorporation of UQ in ML. These guidelines aim to help developers navigate through the field of UQ in ML and support them in ensuring that UQ is applied correctly. DIN SPEC 92005 can be accessed free of charge here.

Challenges

As mentioned before, UQ in ML is actively researched and new ideas are developed to address existing difficulties. One of the current challenges is simultaneous and efficient quantification of both types of uncertainty. Many existing methods capture only one type of uncertainty and combing them leads to increased complexity and, in many cases, also elevated computational cost. Approaches such as deterministic UQ [3] or evidential deep learning [4] aim to solve this problem. Another challenge that can be observed is still relatively low awareness and lack of wide adoption of UQ in AI solutions. Developers and users often rely on (uncalibrated) classification scores which can introduce risk due to overconfidence. In regression tasks, outputs of ML models are usually limited to point estimates without any quantification of uncertainty. Finally, UQ research for rapidly evolving LLMs, is in its early phase and therefore remains a challenge.

Summary

UQ is an important building block of AI safety which is also vital for various other ML techniques such as active learning. Calibrated uncertainty measures can improve decision-making and trustworthiness during operation and therefore offer a step forward beyond offline performance evaluation. Attention and awareness of UQ is growing in scientific and standardization communities as well as industry.  As the field of UQ in ML becomes more technically mature and witnesses growing adoption in 
mission-critical ML tasks, the importance of UQ for safety and certification of AI systems will rise which will help to establish a strong base for the trustworthiness of AI in our society.

If you would like to know more about IABG’s experience with UQ in ML, exchange on this topic or discuss how UQ could be used in your work, feel free to reach out to our safeAI team!